Foire aux questions (F.A.Q.)

  • USGS (United States Geological Survey)
  • IRIS (Incorporated Research Institutions for Seismology)
  • IRSN (Institut de Radioprotection et de Sûreté Nucléaire)
  • Les séismes, Planète Terre (Département de Géologie et de Génie géologique de l'Université de Laval, Québec)
  • Comprendre les séismes, Musée de Sismologie et collections de Géophysique, Université de Strasbourg
  • Musée de sismologie, EOST (École et Observatoire des Sciences de la Terre), Université de Strasbourg
  • Découvrir les séismes Téléchargez le poster réalisé à l'occasion de la 51e bourse aux minéraux de Sainte-Marie-Aux-Mines
  • Quand la terre tremble, C'est pas sorcier, le magazine de la découverte et de la science.

Moment sismique

Chacunes des échelles de magnitude mentionnées ci-dessus a ses restrictions. En outre ces échelles sont sujettes à une forme de saturation, c'est à dire qu'au dessus d'une certaine valeur, la magnitude déterminée est trop faible. La valeur limite au-delà de laquelle la magnitude est inexacte se trouve aux environs de 6.0 pour la magnitude locale calculée sur les ondes de volume. La magnitude de surface sature à partir de 7.5.

Le paramètre physique le plus adéquat pour décrire la "grandeur" d'un séisme est le moment sismique introduit par Aki en 1966. Le moment sismique est directement lié aux dimensions de la source sismique et a été défini comme:

$$M_{0} = \mu \cdot L \cdot W \cdot D$$

où:

  • μ : la rigidité du milieu ou la résistance de la croûte terrestre dans la zone de foyer (~ 3 x 1010 N.m-2);
  • L et W: la longueur et la largeur de la zone de rupture, la partie de la faille qui s'est déplacée durant le séisme. (« la largeur » est la distance mesurée le long de la pente de la faille et la longueur est mesurée transversalement);
  • D: Le déplacement moyen des deux blocs le long de la faille.

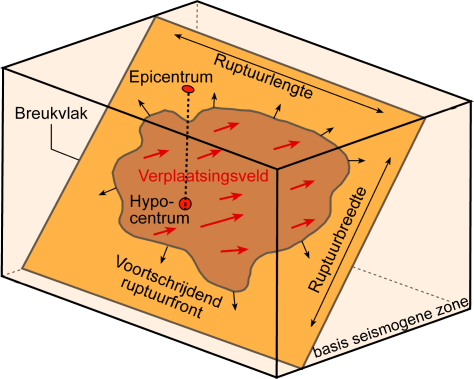
Parametres de la source sismique

Le moment sismique est exprimé en N.m, et peut être calculé à différents endroits des simogrammes enregistrés. Lors des grands séismes, on peut aussi le déterminer, d'une façon indépendante, sur base des indices géodétiques et/ou géologiques de la déformation de la surface terrestre.

Afin de remédier aux restrictions des échelles de magnitude existantes, Kanamori a introduit une nouvelle échelle de magnitude en 1977 sur base du moment sismique. La magnitude de moment est calculée selon une formule logarithmique qui produit des valeurs en accord avec les autres échelles de magnitude pour les magnitudes les plus faibles:

$$M_{W} = \frac{2}{3} log_{10}(M_{0}) - 6.06$$

Une progression d'une unité de magnitude correspond environ à une augmentation du moment sismique. Par opposition aux autres échelles de magnitude, la magnitude de moment est aussi adaptée aux plus grands séismes et cela sans saturation.

Autre manière de l'expliquer : IRSN