Méthode probabiliste
Dans la méthode probabiliste, l'aléa sismique peut être calculé comme étant fonction de la probabilité que survienne un séisme d'une magnitude donnée sur l'échelle de Richter et de la probabilité que soit atteint un niveau donné d'accélération du sol en fonction de la distance et de la magnitude du séisme. Cette méthode permet aux séismologues d’évaluer le mouvement maximal du sol pouvant se produire durant une certaine période de temps choisie en fonction du danger potentiel. Alors que pour les bâtiments ordinaires, il est calculé le plus souvent pour une période de retour de 475 ans, pour les installations sensibles, on considère une plus longue période de retour: p.ex. au moins 10.000 ans pour les centrales nucléaires. Les ingénieurs peuvent alors concevoir ou adapter la construction pour qu'elle résiste à ce niveau de mouvement du sol maximal.
Le calcul s'effectue en plusieurs étapes:
-
Dans une 1ère étape les zones de sources sismiques
sont délimitées. Ce sont des zones présentant une certaine activité sismique
et pour lesquelles on admet que des tremblements de terre s'y produiront
aussi dans le futur. On admet qu'à l'intérieur de chaque zone, les
caractéristiques des séismes et la probabilité qu'ils surviennent sont
constantes.
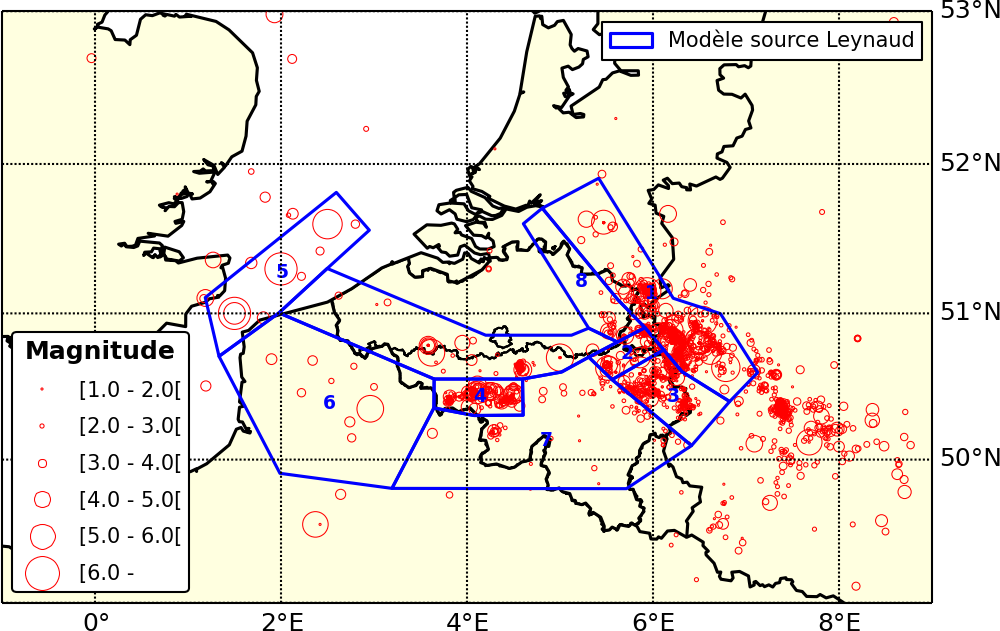
Figure 1 - Zones des sources sismiques en Belgique et environs selon le modèle de Leynaud. On distingue 9 zones: le graben de la Roer (1), Liège-Fourons (2), les Hautes Fagnes (3), le Hainaut (4), le Pas-de-Calais (5), le massif du Brabant (6), l’Artois (7), les Ardennes (8) et le Limbourg (9). Ce modèle de zonage des sources sismiques a été appliqué pour les calculs de l’Eurocode 8; depuis, deux nouveaux zonages ont été développés, qui recouvrent l’ensemble du territoire.
-
Dans une 2ème étape, on détermine l'activité sismique de
chaque zone: à quelle fréquence des séismes d'une magnitude donnée
s'y produisent-ils, quelle est leur profondeur moyenne, quelle est la
magnitude la plus élevée qu'on puisse attendre ? Pour chaque zone, on
calcule la relation entre la fréquence des séismes (nombre/an) et la
magnitude. Cette relation est également appelée « loi » de Gutenberg-Richter.
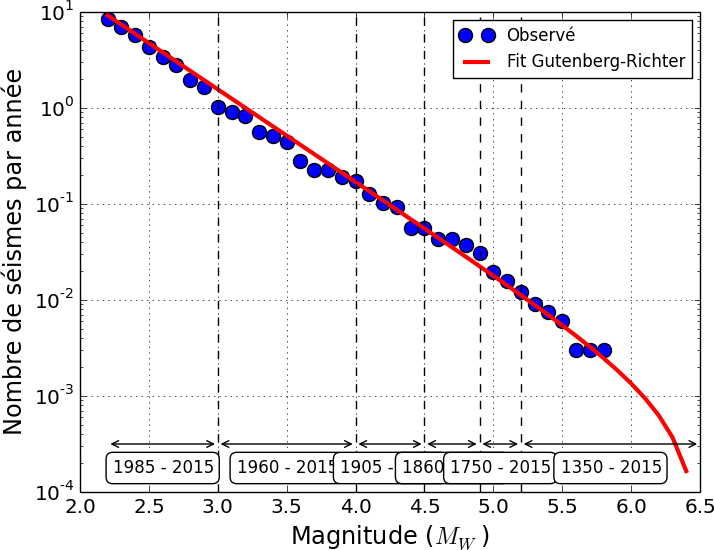
Figure 2 - Relation entre la fréquence des tremblements de terre et la magnitude, pour la Belgique et les régions limitrophes. Des séismes d'une magnitude ≥3 se produisent environ tous les deux ans ; quant aux séismes de magnitude supérieure ou égale à 5, ils se reproduisent en moyenne tous les 50 ans
-
Dans une 3ème étape, on prend en compte un modèle des
mouvements du sol (ou modèle d'atténuation), qui calcule
l'accélération du sol en un endroit donné en fonction de sa distance
épicentrale et de la magnitude du tremblement de terre. Les observations
montrent cependant que l'accélération au sol peut varier fortement pour des
magnitudes et des distances comparables, ce qui rend les incertitudes assez
élevées.
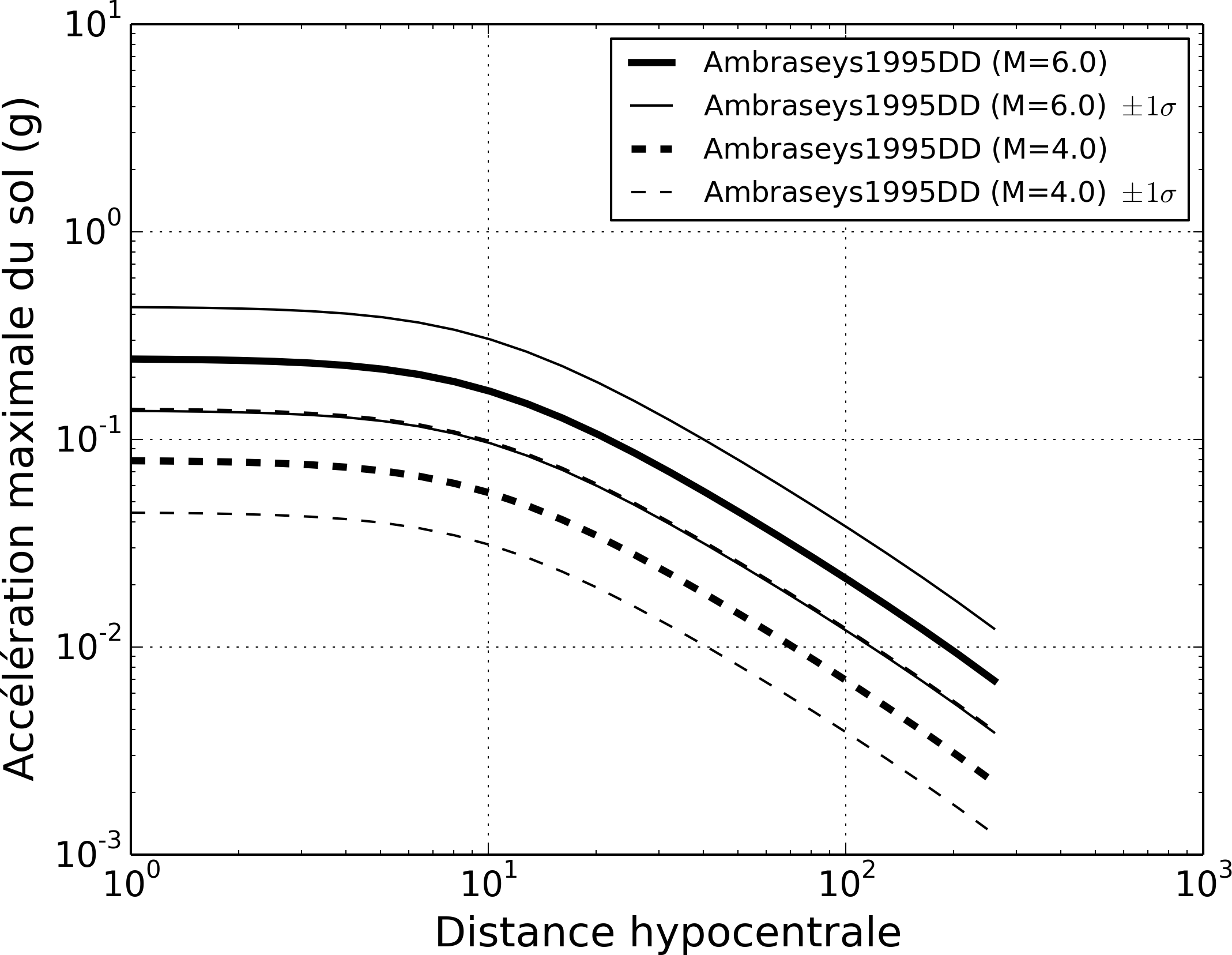
Figure 3 - Relation entre l'accélération maximale au sol et la distance épicentrale pour des séismes d'une magnitude 4 et d'une magnitude 6 à une profondeur de 10 km, selon la loi d'atténuation d'Ambraseys (1995). Cette loi d’atténuation a été appliquée lors des calculs de l’Eurocode 8; cependant, lors d’études plus récentes, l’on utilise la plupart du temps d’autres modèles de mouvements du sol récemment développés
